Wednesday, March 31, 2010
GRE Math Problem 58
A prize of $240 is divided between two persons. If one person receives $180, then what is the difference between the amounts received by the two persons?
(A) $30
(B) $60
(C)$120
(D)$210
(E)$420
Solution for GRE Math Problem 57:
Let’s take three consecutive integers: n-1, n, n+1
Their sum is n-1 + n + n+1 = 3n – is a multiple of 3.
Among the numbers given, only 28 is not the multiple of 3.
Answer:(C) 28
Tuesday, March 30, 2010
GRE Math Problem 57
Which of the following CANNOT be expressed as the sum of three consecutive integers?
(A) 18
(B) 24
(C) 28
(D) 33
(E) 36
Solution for GRE Math Problem 56:
What was Camille's total score?
75x6=450
What was Camille's total score after her teacher had dropped her lowest grade?
85x5=425
What was her lowest grade?
450-425=25
Answer:(B) 25
Monday, March 29, 2010
GRE Math Problem 56
Camille's average on her 6 math tests this marking period is 75. Fortunately for Camille, her teacher drops each student's lowest grade, and this raises her average to 85. What was her lowest grade?
(A) 20
(B) 25
(C) 30
(D) 40
(E) 50
Solution for GRE Math Problem 55:
The average of a, b, c, d, e,f, and g equals to their sum, divided by their quantity. So,
Answer: A
Sunday, March 28, 2010
GRE Math Problem 55
| Column A | Column B |
| The average (arithmetic mean) of a, b, c, d, e,f, and g | 50 |
Solution for GRE Math Problem 54:
In a right triangle with the catheti of 3 and 4, the hypotenuse is 5. But there is no sign indicating that the triangle shown is the right one. So, c can be both greater than 5 (if the angle between the sides of 3 and 4 is obtuse) and less that 5 (if the angle is accute)
Answer: D
Saturday, March 27, 2010
GRE Math Problem 54
Compare:
| Column A | Column B |
c
|
5
|
Solution for GRE Math Problem 53:
As the
point (a,b) lays on the positive direction of X axis, a>0, b=0.
As the
point (c,d) lays on the negative direction of Y axis, c=0, d<0
Then a +
b=a>0 and c + d=d<0 and a + b> c + d
Answer:A
Friday, March 26, 2010
GRE Math Problem 53

| Column A | Column B |
| a + b | c + d |
Solution for GRE Math Problem 52:
In order to solve this, we should know about similarity of geometry figures. If the dimensions of the rug are in the same ratio as those of the floor, they are called similar rectangles. And the areas of similar figures are in the same ratio as the squares of their linear measures. => The linear measures of similar figures are in the same ratio as the square roots of theis areas. Here we have, that the area of the rug is twice smaller, that the floor, then, its length will be √2 times smaller, than the length of the floor. This gives us
Answer:(D)
Thursday, March 25, 2010
GRE Math Problem 52
A rectangular rug covers half of a rectangular floor that is 9 feet wide and 12 feet long. If the dimensions of the rug are in the same ratio as those of the floor, how many feet long is the rug?
(A) 6
(B)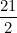
(C)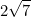
(D)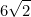
(E)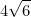
Solution for GRE Analytical Problem 4:
Let’s arrange data and write down requirements and restrictions
Requirement 4: 9Y
Restriction 3: NOT P-G
And we can fill in the table using the requirements 2, 3, 4:
Then, using the Restrictions 2 and 3, we can say that neither 3, nor 5 can be Purple.
Question I. If one of the red pieces is the number 3, what number is the other red piece?
According to Requirement 1: R-R, number 2 must be Red.
Answer: (A) 2
Question II. If the number 5 is green, each of the following could be true EXCEPT
Answer: (B) The number 6 is purple. – This statement contradicts Restriction 2: NOT G-P
Question III. If the number 6 is green, which of the following could be true?
If 6G, we’ll have only two places for the Purple piece: 2 or 8 . If 2P, then we’ll have two consecutive slots for R-R, it is 7-8. Two remaining slots will be taken by the Blue pieces
If 8G, we’ll have only two places for the Purple piece. If 2P, then the two consecutive slots for R-R are 2-3. Two remaining slots will be taken by the Blue pieces
Now let’s look trough the answers
(A) The number 2 is blue. - impossible
(B) The number 3 is purple. - impossible
(C) The number 5 is red. - impossible
(D)The number 5 is purple. - impossible
(E) The number 7 is blue. – possible within the second arrangement
Answer: (C) The number 5 is red (Thanks to swath for correction).
Question IV. Which of the following, if true, would enable you to determine the color of every number?
Let’s first find the statement, which involves the color and location with more restrictions. Let’s test (E) The 7 is green.
Restriction 2: NOT G-P and Restriction 3: NOT P-G leave only one slot for P: 2P
Now we have only single pair of consecutive slots for R-R
And the remaining slots will be taken by B:
So, using statement (E) we managed to determine the colors of all the pieces
Answer: (E) The 7 is green.
Answer:
(A) 6
(B)
(C)
(D)
(E)
Solution for GRE Analytical Problem 4:
Let’s arrange data and write down requirements and restrictions
- One piece is purple and two pieces each are red, green, yellow, and blue.
- The two red pieces are consecutive numbers.
- The number 4 is green.
- The two blue pieces are not consecutive numbers.
- Both the 1 and the 9 are yellow.
Requirement 4: 9Y
- The purple piece is not a number immediately greater than or less than either green piece.
Restriction 3: NOT P-G
And we can fill in the table using the requirements 2, 3, 4:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | G | Y |
Question I. If one of the red pieces is the number 3, what number is the other red piece?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | R | G | Y |
Answer: (A) 2
Question II. If the number 5 is green, each of the following could be true EXCEPT
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | G | G | Y |
Question III. If the number 6 is green, which of the following could be true?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | G | G | Y |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | P | B | G | B | G | R | R | Y |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | R | R | G | B | G | B | P | Y |
(A) The number 2 is blue. - impossible
(B) The number 3 is purple. - impossible
(C) The number 5 is red. - impossible
(D)The number 5 is purple. - impossible
(E) The number 7 is blue. – possible within the second arrangement
Answer: (C) The number 5 is red (Thanks to swath for correction).
Question IV. Which of the following, if true, would enable you to determine the color of every number?
Let’s first find the statement, which involves the color and location with more restrictions. Let’s test (E) The 7 is green.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | G | E | Y |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | P | G | E | Y |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | P | G | R | R | E | Y |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Y | P | B | G | R | R | E | B | Y |
Answer: (E) The 7 is green.
Answer:
Tuesday, March 23, 2010
Analytical Problem 4
John purchased a toy for his young daughter. The toy included nine colorful plastic pieces in the shape of the numbers from 1 to 9. In examining these pieces he made the following observations:
- One piece is purple and two pieces each are red, green, yellow, and blue.
- The two red pieces are consecutive numbers.
- The number 4 is green.
- The two blue pieces are not consecutive numbers.
- Both the 1 and the 9 are yellow.
- The purple piece is not a number immediately greater than or less than either green piece.
Question I. If one of the red pieces is the number 3, what number is the other red piece?
(A) 2 (B) 4 (C) 5 (D) 6 (E) 7
Question II. If the number 5 is green, each of the following could be true EXCEPT
(A) The purple piece and one of the yellow piece are consecutive numbers.
(B) The number 6 is purple.
(C) The two blue pieces and the purple piece are three consecutive numbers.
(D) The number 2 is red.
(E) The number 8 is red.
Question III. If the number 6 is green, which of the following could be true?
(A) The number 2 is blue.
(B) The number 3 is purple.
(C) The number 5 is red.
(D)The number 5 is purple.
(E) The number 7 is blue.
Question IV.Which of the following, if true, would enable you to determine the color of every number?
(A) The 2 is blue.
(B) The 3 is blue.
(C) The 5 is red.
(D)The 7 is blue.
(E) The 7 is green.
Solution for GRE Math Problem 51:
If we take the second researcher's time as 100%, the first one's time will be 75%. Therefore, the ratio is 75:100=3:4. So, we should divide 35 into the ratio of 3:4. We'll get 15 and 20, their difference is 20-15=5<7
Answer:B
Sunday, March 21, 2010
GRE Math Problem 51
Two researchers spent a total
of 35 hours on a certain project. One of the researchers spent 25 percent fewer
hours on the project than the other.
Solution for GRE Math Problem 50:
The sandwich with, let's say, lattuce on onion and the the sandwich with onion on lattuce are different sanwiches. So, to calculate the total number of sandwiches, we should use arrangements, not combinations. number of arrangement of m items out of n ones is A(n,m)=n!/(m-n)!=n*(n-1)*(n-2)*...*(n-m+1) A(4,1)=4 A(4,2)=4*3=12 A(4,3)=4*3*2=24 A(4,4)=4*3*2*1=24 Total 24+24+12+4=64>32. Answer:A
| Column A | Column B |
| The difference between the number of house spent by each | 7 |
Solution for GRE Math Problem 50:
The sandwich with, let's say, lattuce on onion and the the sandwich with onion on lattuce are different sanwiches. So, to calculate the total number of sandwiches, we should use arrangements, not combinations. number of arrangement of m items out of n ones is A(n,m)=n!/(m-n)!=n*(n-1)*(n-2)*...*(n-m+1) A(4,1)=4 A(4,2)=4*3=12 A(4,3)=4*3*2=24 A(4,4)=4*3*2*1=24 Total 24+24+12+4=64>32. Answer:A
Saturday, March 20, 2010
GRE Math Problem 50
A vegetarian sandwich shop has
a choice of 4 different sandwich toppings.
Solution for GRE Math Problem 49:
There is the possibility for m=5 ,n=5, thus m=n. But there also can be m=1, n=25 and m
In general, the relation is unknown.
Answer:D
| Column A | Column B |
| The number of different types of sandwiches that can be made if at least one topping has to be used and each topping cannot be used more than once. | 32 |
Solution for GRE Math Problem 49:
There is the possibility for m=5 ,n=5, thus m=n. But there also can be m=1, n=25 and m
In general, the relation is unknown.
Answer:D
Wednesday, March 17, 2010
GRE Math Problem 49
m and n are positive integers mn = 25
Solution for GRE Math Problem 48:
Putting r=0, t=0 we have 0=0. Putting r=1, t=1 we have 10 > 6
Answer: D, unable to determine
| Column A | Column B |
| m | n |
Solution for GRE Math Problem 48:
Putting r=0, t=0 we have 0=0. Putting r=1, t=1 we have 10 > 6
Answer: D, unable to determine
Tuesday, March 16, 2010
GRE Math Problem 48
Compare:
Solution for GRE Math Problem 47:
x(x + y) + y(x + y) = (x+y)(x+y) = (x + y)2
Answer:C, they are equal
| Column A | Column B |
| 5(r +t) | 5r + t |
Solution for GRE Math Problem 47:
x(x + y) + y(x + y) = (x+y)(x+y) = (x + y)2
Answer:C, they are equal
Monday, March 15, 2010
GRE Math Problem 47
Compare:
Solution for GRE Math Problem 46:
(a + 2)(b + 3)=ab+3a+2b+6
(a + 3)(b + 2)=ab+2a+3b+6
Let's find the difference:
(a + 2)(b + 3)–(a + 3)(b + 2) = ab+3a+2b+6 – (ab+2a+3b+6) = a–b
Since there are no restrictions for a and b, their difference can have any sign, then, answer is D, unable to determine
Answer:D
| Column A | Column B |
| (x + y)2 | x(x + y) + y(x + y) |
Solution for GRE Math Problem 46:
(a + 2)(b + 3)=ab+3a+2b+6
(a + 3)(b + 2)=ab+2a+3b+6
Let's find the difference:
(a + 2)(b + 3)–(a + 3)(b + 2) = ab+3a+2b+6 – (ab+2a+3b+6) = a–b
Since there are no restrictions for a and b, their difference can have any sign, then, answer is D, unable to determine
Answer:D
Sunday, March 14, 2010
GRE Math Problem 46
Compare:
Solution for GRE Math Problem 45:
Just make calculations: 2*3+3*2=12
Answer: (C) 12
| Column A | Column B |
| (a + 2)(b + 3) | (a + 3)(b + 2) |
Solution for GRE Math Problem 45:
Just make calculations: 2*3+3*2=12
Answer: (C) 12
Saturday, March 13, 2010
GRE Math Problem 45
6. If x = 3 and y = 2, then 2x + 3y =
(A) 5
(B)10
(C)12
(D)14
(E)15
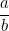 , is bigger than
, is bigger than  if a > 2b and less than
if a > 2b and less than  otherwise. The only fraction here which is less than
otherwise. The only fraction here which is less than 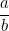 is (E)
is (E) 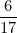
Answer: E
(A) 5
(B)10
(C)12
(D)14
(E)15
Solution for GRE Math Problem 44:
The fractionAnswer: E
Friday, March 12, 2010
GRE Math Problem 44
Which of the following fractions is the LEAST?
(A)
(B)
(C)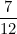
(D)
(E)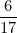
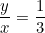 , then x=3y. Putting this to 3x-4y=5, we’ll get 9y-4y=5, y=1. Therefore, x=3
, then x=3y. Putting this to 3x-4y=5, we’ll get 9y-4y=5, y=1. Therefore, x=3
Answer:(D)
(A)
(B)
(C)
(D)
(E)
Solution for GRE Math Problem 43:
AsAnswer:(D)
Thursday, March 11, 2010
GRE Math Problem 43
If 3x-4y=5 and 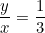 then what is x?
then what is x?
(A)-5y
(B)-5x
(C)1
(D)3
(E) 4
Answer:(B)
(A)-5y
(B)-5x
(C)1
(D)3
(E) 4
Solution for GRE Math Problem 42:
bd=3ax3c=3a+cAnswer:(B)
Wednesday, March 10, 2010
GRE Math Problem 42
If 3a=b and 3c=d, then bd=
(A) 3ac
(B) 3a+c
(C) 6a+c
(D) 9ac
(E) 9a+c
Solution for GRE Math Problem 41:
Let’s build this sequence: 1, 1x3-1=2, 2x3-1=5, 5x3-1=14, 14x3-1=41, 41x3-1=122 – this is the smallest term greater than 100. It is greater than 120
Answer:A
(A) 3ac
(B) 3a+c
(C) 6a+c
(D) 9ac
(E) 9a+c
Solution for GRE Math Problem 41:
Let’s build this sequence: 1, 1x3-1=2, 2x3-1=5, 5x3-1=14, 14x3-1=41, 41x3-1=122 – this is the smallest term greater than 100. It is greater than 120
Answer:A
Tuesday, March 9, 2010
GRE Math Problem 41
The first term of a sequence is 1. Starting with the second term, each term is 1 less than 3 times the previous term.
Solution for GRE Math Problem 40:
As we can see, the sum of the areas of two equilateral triangles whose sides are 10 is twice less than the area of one equilateral triangle whose sides are 20
Answer:B
| Column A | Column B |
| The smallest number greater than 100 in the sequence | 120 |
Solution for GRE Math Problem 40:
As we can see, the sum of the areas of two equilateral triangles whose sides are 10 is twice less than the area of one equilateral triangle whose sides are 20
Answer:B
Monday, March 8, 2010
GRE Math Problem 40
| Column A | Column B |
| The sum of the areas of two equilateral triangles whose sides are 10 | The area of one equilateral triangle whose sides are 20 |
Solution for GRE Math Problem 39:
If x was 90, AB would be a hypotenuse in the right isosceles triangle and its value would be
And for x > 90, AB will be even longer.
Answer: A
Sunday, March 7, 2010
GRE Math Problem 39
x>90
Solution for GRE Math Problem 38:
How many three-digit numbers are?
The first digit can be any of 9, the second - any of 10, so does the third. Total 9x10x10=900 combinations.
How many three-digit palindromes are?
The first digit can be any of 9, the second - any of 10, and the third one must be exactly the same as the first, thus, leaving only 1 possibility. Total 9x10x1=90.
The probability that a three-digit number chosen at random is a palindrome is 90x900=0.1
Answer: C
| Column A | Column B |
The length of AB | 7 |
Solution for GRE Math Problem 38:
How many three-digit numbers are?
The first digit can be any of 9, the second - any of 10, so does the third. Total 9x10x10=900 combinations.
How many three-digit palindromes are?
The first digit can be any of 9, the second - any of 10, and the third one must be exactly the same as the first, thus, leaving only 1 possibility. Total 9x10x1=90.
The probability that a three-digit number chosen at random is a palindrome is 90x900=0.1
Answer: C
GRE Math Problem 38
A number is a palindrome if it reads exactly the same from right to left as it does from left to right.
For example, 959 and 24742 are palindromes.
| Column A | Column B |
The probability that a three-digit number chosen at random is a palindrome | 0.1 |
Solution for GRE Math Problem 37:
If all 16 shirts had costed $10, total amount of money spent would have been $160. It is $27 less, than the actual amount. Since Each $13 shirt is $3 more expensive than $10 shirt, there were 9 $13 shirts and 7 $10 shirts
Answer: A
Friday, March 5, 2010
GRE Math Problem 37
A man buys 16 shirts. Some of them cost $13 each, while the remainder cost $10 each. The cost of all 16 shirts is $187.
Solution for GRE Math Problem 36:
If all the tickets hab been sold for $25, the total sum would be 25x11=$275, which is 275-227=.$48 less, than the actual amount of money. Since the $13 ticket is 25-13=$12 cheaper, theree were = 4 tickets for $13 and 11-4=7 tickets for $25.
Answer: Column A is bigger
| Column A | Column B |
The number of $13 shifts purchased | The number of $10 shirts purchased |
Solution for GRE Math Problem 36:
If all the tickets hab been sold for $25, the total sum would be 25x11=$275, which is 275-227=.$48 less, than the actual amount of money. Since the $13 ticket is 25-13=$12 cheaper, theree were = 4 tickets for $13 and 11-4=7 tickets for $25.
Answer: Column A is bigger
Tuesday, March 2, 2010
GRE Math Problem 36
Tickets to a concert cost $25 and $13. An agent sells 11 tickets for a total price of $227.
Solution for GRE Math Problem 35:
If a2=b, then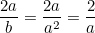 .
.
Now, if a=1, then Column A = 2 > Column B = 1.
And if a=2, then Column A = 1 < Column B = 4.
Answer: D, unable to define.
| Column A | Column B |
The number of $25 tickets sold | The number of $13 tickets sold |
Solution for GRE Math Problem 35:
If a2=b, then
Now, if a=1, then Column A = 2 > Column B = 1.
And if a=2, then Column A = 1 < Column B = 4.
Answer: D, unable to define.
Subscribe to:
Comments (Atom)







